SPIELMÖGLICHKEITEN: Freies Spiel | Einmaleins | Einmaleins mit Rechnen | Knobeltürmchen | Rechenmaschine
Wie, – das geht?!
sortieren wir die 100 Klötzchen zur großen Quoai-Treppe.
Dann bekommt jeder Stein, vom kleinsten bis zum größten einen Namen angedichtet. Was den Kindern gerade zu den Zeichen auf der Stirnseite einfällt: Drache, Schild, Topf, Blume, Tannenbaum, Batman, usw.
Mit Engagement und Gelassenheit verhandeln Vorschul- sowie Grundschulkinder untereinander, welcher Name am besten passen würde.
Kein Streit, kein Gerangel. Volles Engagement.
Besuch einer Schweizer Grundschule, 1. Klasse
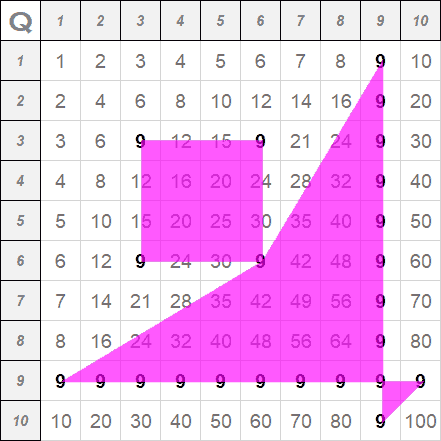
Die große Quoai-Treppe bildet das Baustofflager. Hier werden die Steine für die einzelnen Reihen entnommen.
Drei Kinder bauen zusammen, immer im Wechsel: das erste zählt, das zweite nimmt und übergibt die Steine und das dritte setzt sie an die richtige Stelle.
Präsentiert es sich allerdings wie ein Gewebe aus Kett- und Schussfäden; oder wie auf eine Schnur gereihte Perlen, wird es für Jene, die noch nicht addieren oder multiplizieren können, ein Kinderspiel.
Wir haben mit Kindern einen Plan entwickelt, um aus den 100 Klötzchen eine Struktur aufzubauen, die dem Einmaleins zugrunde liegt. Dabei orientieren sie sich im Raum und in der Fläche, arbeiten im Team und dürfen weiter ihre Fantasie walten lassen.
Hier geht es ums Zählen und Wahrnehmen von Relationen, Strukturen, Größen und Mustern. Die Feinmotorik kommt dabei nicht zu kurz.
Dieses Tun bringt Erwachsene und Kinder zusammen, denn es ist für Beide erstaunlich, diese Symmetrien zu entdecken.
Im Zählkreis wird abgezählt, welche Klötzchen vom Baustofflager entnommen werden.
Besuch in einer Schweizer Grundschule, 1. Klasse
Leerstelle Kunst – 32. Landesweite Kunstschau 2022 Ausstellung des Künstlerbundes Mecklenburg und Vorpommern e. V. im BBK
Die erste Reihe ist die Einerreihe.
Wir beginnen beim ersten Klötzchen des Abzählkreises.
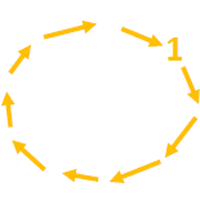Das zählende Kind geht mit dem Finger in Einerschritten den Klötzchenkreis im Uhrzeigersinn entlang – über die Neun hinweg! – bis es auf zehn Klötzchen gewiesen hat, die dann die beiden anderen dem Baustofflager entnehmen und in einer aufsteigenden Reihe vor sich aufstellen.
Die Zweierreihe:
Wir beginnen beim zweiten Klötzchen.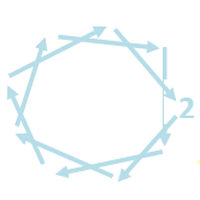
Jetzt geht es in Zweierschritten im Uhrzeigersinn voran – über die Neun hinweg – bis 10 Klötzchen abgezählt sind.
Die entsprechenden Klötzchen werden der großen Treppe entnommen und neben der Einerreihe aufgestellt.
Die Dreierreihe:
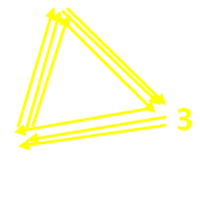Wir beginnen beim dritten Klötzchen, überspringen immer zwei, über die Neun hinweg, bis zehn Klötzchen abgezählt sind.
Der großen Treppe werden die entsprechenden Klötzchen entnommen und neben der Zweierreihe aufgestellt.
Die Viererreihe:
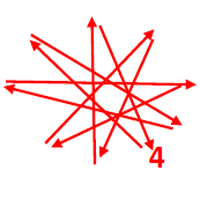Wir beginnen beim vierten Klötzchen, überspringen immer drei, über die
Neun hinweg, bis wir zehn Klötzchen haben.
Wir entnehmen der großen Treppe die entsprechenden Klötzchen und stellen sie neben die Dreierreihe.
Die Fünferreihe:
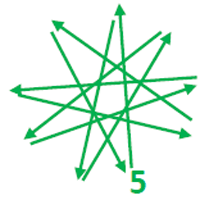
Wir beginnen beim fünften Klötzchen, überspringen immer vier, über die
Neun hinaus, bis wir zehn Klötzchen gezählt haben.
Wir entnehmen die entsprechenden Klötzchen und stellen sie neben die Viererreihe.
Die Sechserreihe:
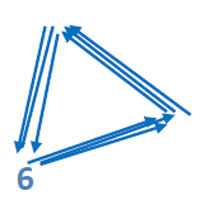Wir beginnen beim sechsten Klötzchen, überspringen immer fünf, über die Neun hinweg, bis wir zehn Klötzchen gezählt haben.
Wir entnehmen der großen Treppe die entsprechenden Klötzchen und stellen sie neben die Fünferreihe.
Die Siebenerreihe:
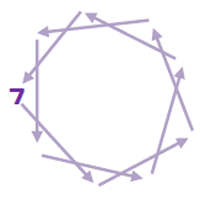Wir beginnen beim siebten Klötzchen, überspringen immer sechs, über die Neun hinweg, bis zehn Klötzchen abgezählt sind.
Der großen Treppe werden die entsprechenden Klötzchen entnommen und neben der Sechserreihe aufgestellt.
Die Achterreihe:
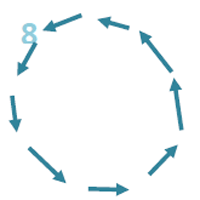Wir beginnen beim achten Klötzchen, überspringen immer sieben, über die
Neun hinweg, bis wir zehn Klötzchen haben.
Wir entnehmen der großen Treppe die entsprechenden Klötzchen und stellen sie neben die Siebenerreihe.
Die Neunerreihe:
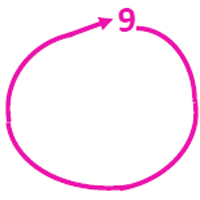Wir beginnen beim neunten Klötzchen, überspringen immer acht, über die Neun hinweg, bis wir zehn Klötzchen gezählt haben.
Wir entnehmen der großen Treppe die entsprechenden Klötzchen und stellen sie neben die Achterreihe.
So wird früh erfahren, was Ordnungszahlen, Vorgänger und Nachfolger sind.
Es gibt merkwürdige Phänomene zu entdecken: Warum ähnelt die Einer-Reihe der Achter-Reihe? Warum sieht die Neuner-Reihe wie eine Stadtmauer aus?
Entfernt man die Neuner- und Zehner-Reihen, bleibt sozusagen der „Kern“, ein Modul, bestehend aus 8 x 8 Klötzchen.
Wird das Ganze entlang der Achsen auseinandergezogen, zeigt sich deutlich die symmetrische Struktur. Hat man so etwas beim Aufbauen geahnt?
