

SPIELMÖGLICHKEITEN: Freies Spiel | Einmaleins | Einmaleins mit Rechnen | Knobeltürmchen | Rechenmaschine
Alle Rechenarten sind möglich!
Wie, – das geht?!

Unser Stellenwertsystem wurde von Menschen entwickelt, die von rechts nach links schrieben. Logischer für das Rechnen mit dem Stellenwertsystem wäre es also, von rechts zu lesen.
Es gibt neun Einer. Der zehnte Einer wandert in die Reihe der Zehner. Hier können wir beobachten, wie der Zehnerübergang „passiert“.
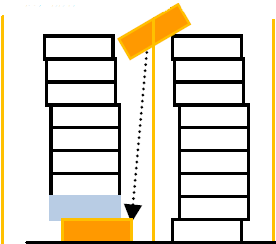
Der zehnte Einer wird zum ersten Zehner. Bei den Einern kommt jetzt die Null ins Spiel. Die neun Einer könnte man die „Fülle des Zehners“ nennen.
Der zweite Zehner, also die Zwanzig (hier der hellblaue Stein) hat ihre neun Einer ebenfalls in der Reihe der Einer. Die neun Einer von 11 bis 19 machen die „Fülle der Zwanzig“ aus. Ebenso verhält es sich mit den Hundertern gegenüber den Tausendern etc.
(Mit Quoai Klötzchen ist das leichter verdaulich als ohne. Für Erwachsene wie für Kinder.)
Sechs Reihen mit Klötzchen von 1 bis 9 nebeneinander aufstellen. Rechts die Zehntel, links davon die Einer, die Zehner, Hunderter, Tausender, Zehntausender. Je nach Belieben erweitern wir links und rechts mit mehr Reihen.
Die konkreten Zahlen der einzelnen Stellen werden mit Erbsen markiert.
Die Null entstand aus der Notwendigkeit, im Stellenwertsystem die Stelle markieren zu können, an der keine Zahl von 1 bis 9 steht. In unserem Spiel eben keine Erbse liegt.

Babylonier, Griechen, Mayas und Chinesen suchten schon lange nach einer Lösung. Letztlich gelang es den Indern vor ca. 2000 Jahren. Schnell verbreitete sich die Neuigkeit in allen asiatischen und arabischen Ländern. In Europa rechnen wir seit ca. 500 bis 800 Jahren mit der Null.
Aufgabe: 6.317 + 7 = ?

Bei den Einern beginnen.
Die Erbse von Stufe 7 um zwei Schritte nach oben versetzen. Hier endet die Reihe der Einer. Wir eröffnen einen neuen Zehner. Die Erbse auf der Zehner-Treppe wandert einen Schritt nach oben. Von 10 nach 20. Dadurch entstehen wieder neun neue Einer. Von den sieben zu gehenden Schritten verbleiben noch vier, da wir zwei Einer-Schritte und den neu eröffneten Zehner schon gezählt haben. Die Erbse der Einer-Treppe wandert also noch von unten vier Stufe nach oben – und wird hier abgelegt.
Ergebnis: 6.324
Aufgabe: 6.317 – 11 = ?

Bei den Einern beginnen.
Die Erbse auf Stufe 7 wird um eins herunter versetzt auf die
6. Stufe. Dann müssen noch zehn abgezogen werden. Die Erbse auf dem ersten Zehner muss weg. Wo keine Erbse liegt, schreiben wir eine Null. Die anderen Erbsen dürfen liegen bleiben.
Ergebnis: 6.306
Aufgabe: 6.317 x 5 = ?

Bei den Tausendern beginnen:
5 x 6 = 30 → Erbse auf Stufe 3 der Zehntausender setzen.
Bei den Hundertern:
5 x 3 = 15 → Eine Erbse auf Stufe 1 der Tausender setzen, andere Erbse auf Stufe 5 der Hunderter.
Bei den Zehnern:
5 x 1 = 5 → Erbse auf Stufe 5 der Zehner.
Bei den Einern:
5 x 7 = 35 → Bei den Zehnern steigt die Erbse um drei Schritte von Stufe 5 auf Stufe 8. Bei den Einern kommt eine Erbse auf Stufe 5.
Ergebnis: 31.585
Aufgabe: 6.317 : 9 = ?

Bei den Tausendern beginnen:
6 : 9 = ? → nicht möglich: wir legen keine Erbse und schreiben keine Null.
Bei den Hundertern: Wir nehmen die sechs des unverbrauchten Tausenders dazu!
63: 9 = 7 → Erbse auf Stufe 7 der Hunderter.
Bei den Zehnern:
1: 9 = ? → nicht möglich: wir legen keine Erbse
Bei den Einern: Wir nehmen die eins der unverbrauchten Zehner dazu!
17 : 9 = 1 → Erbse auf die 1; es bleibt der Rest acht.
Wer es schon kann, errechnet die Stellen hinter dem Komma. Denn rechts von den Einern passiert auch noch etwas….
Ergebnis: 701 Rest 8
Dieses Spiel macht Spaß. Damit erklärt sich das Stellenwertsystem, die Null und das schriftliche Rechnen mit größeren Zahlen.